The equals sign does not mean the answer comes next!

As part of the team who worked on developing Elementary Mathematics Professional Learning Opportunities (EMPL), I spent a significant amount of time learning about the importance of Equality and have presented many times across Alberta on this topic using the resources and research we compiled through the project. A recent comment on Facebook made me aware that I should write a blog post about this too! If you've visited the Equality portion of the EMPL site, you will see that this post is a compilation of a part of those resources. Note: All images that contain the EMPL logo are pulled from the presentation document that we developed.

Our team defined 3 big ideas around Equality. 

1. Mathematically, equality refers to a relationship between objects that can be quantified.
2. Mathematically, equality can refer to a relationship between units of measure.
3. Operations emerge as a way to balance an inequality.

This post will focus on the first big idea: "Mathematically, equality refers to a relationship between objects that can be quantified."

I use the term "objects" loosely. In the beginning, students will be considering and using concrete objects (bears, counters, beans, etc.). As their understanding progresses, they will move on to more abstract representations of those same objects. Even in higher grades, when you are referring purely to a symbolic representation such as an algebraic expression, it still refers to objects of some kind.  You’ve abstracted the objects out of the equation. Please don't get hung up on the terminology or lack thereof that I have used here. Let's look at the bigger picture and then we can always return to the tendency, preference and need we have to define terminology more explicitly.  :)

Before we start, please jot down a simple addition or subtraction equation that you would ask students to solve in a K-4 classroom. We will come back to this question later.

Take a moment to think about the following: 

How would your students answer this question? "What does the equal sign mean?"

I would recommend going into your classroom and asking your students that question. Ask it in grade 2. Ask it in Grade 6. Ask it in high school. Just ask. I'll wait. Come back when you are ready...

Researchers asked students this very question. They looked at students' responses and determined that there were two kinds of understanding.

One is an "operational understanding". Students who have an operational understanding of the equals sign might respond by saying...

These students believe the equal sign means "add the numbers" or "the answer".

How might an "Operational" student respond when asked to complete the following statement to make it true?  

3 + 2 = __ + 1

Most operational thinking students will put a 5 here because 3 + 2 = 5.

Some will even continue and tell you the answer, therefore, is 6 because 5 + 1 = 6.

The other type of understanding is a "relational understanding". Students who have a relational understanding of the equals sign might respond by saying...

These students see the equal sign as an equivalence relation between two quantities.

How might a "Relational" student respond when asked to complete the following statement to make it true?

3 + 2 = __ + 1

Relational thinking students will write a 4 here because 3 + 2 = 5 and 4 + 1 = 5

Researchers asked students to do the following:

Make this statement true.

8 + 4 = __ + 5

What percent of your students do you believe would get this right? What other answers do you think you might get? Now, without pre-teaching anything or having a prior discussion, give this question to your students and see how they respond. Their answers will tell you a lot about their understanding of equality and the equals sign.

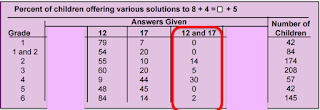
Let's take a look at the results.

How would "Operational" students respond? 

They may have answered 12. The numbers below indicate the percent of students who gave this response.

"Operational" students may have also responded with 17. How do you think they arrived at that answer?

Some even wrote both 12 (in the first blank) and then = 17 at the end.

What percent responded correctly with the answer 7? 

"Other" refers to any answer given that was not one of the four previously discussed.

If we choose to believe the results from the research study are still accurate today, about how many students in your class truly understand the equals sign? I strongly recommend that you give this question to your students to see how they respond.

So what do we do?

Let's look at Equality as a quantity through a few True or False questions. I've included images from the EMPL presentations, but you should use concrete objects for students to look at when doing this activity in your class. 

This one should be pretty easy for both you and your students. I would say something like, "The first set has a quantity of 3. The second set has a quantity of 3. They both of a quantity of 3. They are equal. Let's replace those quantities with their symbols. There are 3 objects on each side.

3 = 3

This is when it gets interesting for students. If they just see 3 = 3, many will tell you this is formatted incorrectly. "We don't write 3 = 3." We need to make sure that students see such basic equations in order to make sure we are not perpetuating the misunderstanding. This is one of the first equations they should learn.

What changed? Are these sets still equal? Let's replace the quantities with their symbols. 

3 = 3

We are still comparing quantities. Therefore the color of the cubes does not change the relationship. This is why it's important to make sure students understand that we are talking about quantity not other characteristics such as color.

What changed? Are these sets still equal? We are still comparing quantities. 

3 = 3

Therefore the elephant still represents one object. This is why it's important to make sure that students understand that we are talking about quantity not other physical characteristics.

What changed? Are these sets still equal? 3 = 3 for the same reasons as above.

What about these sets? Are they equal? Yes, these are still sets. They are just sets of nothing. Students need to understand that it's ok to say 0 = 0.

I think you get the idea. Let's move on to the next stage of building understanding of the equals sign.

Let's jump back to one set for now. You could do this at this stage or before completing the previous activity.

How many dots are there? How do you know? Johnny may have seen it as 3 +3 (write that) while Lisa saw it as 1 + 4 + 1 (write that beside the 3 + 3). Did they see the same amount? Yes. Write the equals sign between the two. Now you have 3 + 3 = 1 + 4 + 1. Reinforce that they are both the same quantities.

Let's move back to comparing two sets.

What's the relationship between these sets? The relationship is equal. How do we record that in math?

We'll start with the total in each. 6 = 6 (same as before). However, we want to take it to the next level. (This should sound familiar...) How did you know there were 6 in the first? Did you just know (subitize) that it was 6? Did you see 3 + 3? 4 + 2? Let's say you just knew it was 6. You subitized it because it looks like the dots on a dice.

What about the ones on the right? Did you know it was 6? Did you see 3 + 3? Did you see 1 + 4 + 1? 1 + 2 + 2 + 1? Let's say you say it as 3 + 3.

How would you record this?

You say the first set as 6 and the second set as 3 + 3 so 6 = 3 + 3.

Remember, students who have an operational understanding will say the equation written in the form 6 = 3 + 3 as written "wrong".

Students could also write this as 4 + 2 = 1 + 4 +1 or 3 + 3 = 3 + 2 +1 or...it all depends on how they saw the first set and how they saw the second set. There are many options.

Now, go back to that question I asked you to write down near the beginning of the blog post. Did you write it in the form of 5 + 6 = ? or 9 - 4 = ? with the "question" on the left and the "answer" as the blank on the right?  Most of our resources show questions in this format. This is one of the reasons why students are led to believe that the equals sign means the answer comes next...because this is the way they have always seen it.

What are some simple ways that you can change this? 

1. Compare how two students saw the same image. Write it as a comparison: 3 + 4 = 2 + 5
2. Instead of always saying "5 + 6 is equal to" try "5 + 6 is the same amount as", "5 + 6 is the same as", and "5 + 6 has the same value as".  Use a different phrase for the equals sign often. You may be worried that students will be confused about the changes in terminology but they won't. Trust them. You can always say "has the same value as...is equal to" the first few times to help them understand the term "value" in this context.
3. Instead of always writing your questions as "5 + 6 = ?", turn it into "? = 5 + 6". You can phrase it as "What is 5 + 6?" as you point to the question mark?
4. When looking at the first set of 6 in the image above, say "There are 6 here." (Write down 6). Ask, "how did you see it?" If they say 3 on the top and 3 on the bottom, say "You saw six as" (write the equals sign) "3 and 3" (write 3 +3 so you now have 6 = 3+ 3)

There are many other activities that will take this to the next level.

Misconceptions about Equality are not easily undone.

What do you do though, when a student says 3 + 2 = 5 + 1? How do you respond? Ask, "What materials could you use to demonstrate this?" Have them build it concretely such as unifix cubes. 

Do the blocks prove this is true or not true?

Does this make it easier to see?

Does turning the blocks change your thinking?

Build the left side of the equation: 3 + 2

Consider the rest of the equation. Using the same blocks, can you represent 5 + 1?

How does this help prove or disprove 2 + 3 = 5 + 1.

All of these ways are valid. Students need more than one way to explain it. Make sure the equation is always in front of them as they manipulate the materials. A student who can conserve 5 should understand this. It's important that they also understand that they can't add extra blocks. Equality is about representing the same quantity in different ways.

If 2 + 3 = 5

and

4 + 1 = 5,

then

2 + 3 = 4 + 1

So, 2 + 3 can not be equal to 5 + 1

If students are struggling in math class, give them the question 8 + 4 = __ + 5. How they answer will tell you if you need to stop what you are doing and deal with any misconceptions they have around the equals sign. Spend the time! How can we expect them to manipulate two step equations if they don't understand that it's about relationships?

Reflection for the Reader:

Are you surprised by the results of the research study? How are you dispelling misconceptions around the equals sign regardless of the grade level you are teaching?